✍️ 八股文 @ 面试手撕

415. 大数相加

腾讯 WXG 一面

给定两个字符串形式的非负整数 num1 和 num2 ，计算它们的和并同样以字符串形式返回。

你不能使用任何內建的用于处理大整数的库（比如 BigInteger），也不能直接将输入的字符串转换为整数形式。

示例 1：

1 2	输入：num1 = "11", num2 = "123" 输出："134"

示例 2：

1 2	输入：num1 = "456", num2 = "77" 输出："533"

1️⃣ 解法一：对位数较短的数字进行了补零操作（预处理）：self-AC

class Solution {
public:
    string addStrings(string num1, string num2) {
        int m = num1.length(), n = num2.length();
        int len = abs(m - n);
        string zero(len, '0');
        if (m < n)
            num1 = zero + num1;
        else if (m > n)
            num2 = zero + num2;
        int mx = max(m, n);
        int remain = 0;
        string ans;
        // cout << num1 << ", " << num2 << endl;
        for (int i = mx - 1; i >= 0 || remain; i--) {
            if (i < 0 && remain) {
                ans.push_back('1');
                break;
            }
            char ch = num1[i] + (num2[i] - '0') + remain;
            if (ch > '9') {
                ch = ch - 10;
                remain = 1;
            } else {
                remain = 0;
            }
            ans.push_back(ch);
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

2️⃣ 解法二：去除预处理的过程，直接模拟

class Solution {
public:
    string addStrings(string num1, string num2) {
        int i = num1.length() - 1, j = num2.length() - 1, add = 0;
        string ans = "";
        while (i >= 0 || j >= 0 || add) {
            int x = i >= 0 ? num1[i] - '0' : 0;
            int y = j >= 0 ? num2[j] - '0' : 0;
            int result = x + y + add;
            ans.push_back('0' + result % 10);
            add = result / 10;
            i--;
            j--;
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }
};

43. 大数相乘

小鹏汽车智驾一面

✅ LeetCode: 43. 字符串相乘

给定两个以字符串形式表示的非负整数 num1 和 num2，返回 num1 和 num2 的乘积，它们的乘积也表示为字符串形式。

**注意：**不能使用任何内置的 BigInteger 库或直接将输入转换为整数。

示例 1:

1 2	输入: num1 = "2", num2 = "3" 输出: "6"

示例 2:

1 2	输入: num1 = "123", num2 = "456" 输出: "56088"

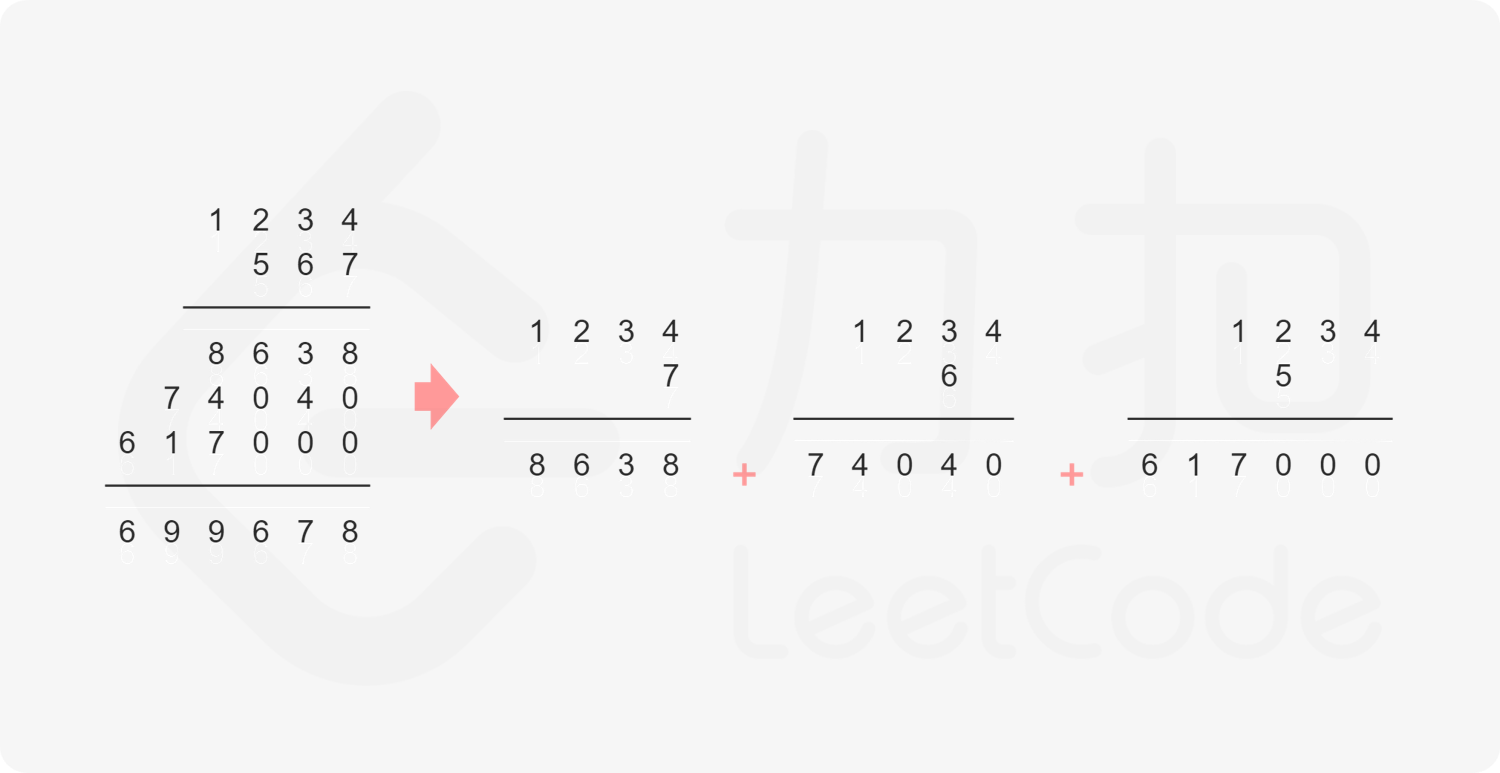
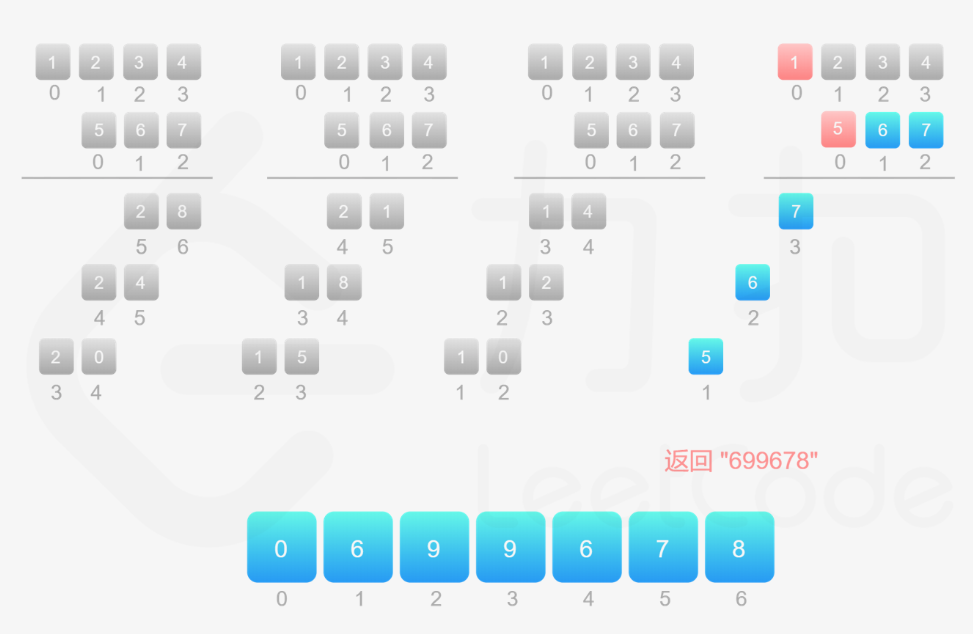
1️⃣ 解法一思路（竖式相加）：建立在「大数相加」的基础上，因为多个数之间需要累加（这段代码自己 AC 的，容易理解）

fig1

class Solution {
public:
    // 大数相加
    string addStrings(string num1, string num2) {
        int i = num1.length() - 1, j = num2.length() - 1, add = 0;
        string ans = "";
        while (i >= 0 || j >= 0 || add) {
            int x = i >= 0 ? num1[i] - '0' : 0;
            int y = j >= 0 ? num2[j] - '0' : 0;
            int result = x + y + add;
            add = result / 10;
            ans.push_back('0' + result % 10);
            i--;
            j--;
        }
        reverse(ans.begin(), ans.end());
        return ans;
    }

    // 大数相乘
    string multiply(string num1, string num2) {
        if (num1 == "0" || num2 == "0")
            return "0";
        int multiply = 0;
        int m = num1.length(), n = num2.length();
        string ans = "0";
        for (int i = m - 1; i >= 0; i--) {
            int x = num1[i] - '0';
            string num;
            int add = 0;
            for (int j = n - 1; j >= 0 || add; j--) {
                if (x == 0) {
                    num = "0";
                    break;
                }
                if (j < 0) {
                    num.push_back('0' + add);
                    break;
                }
                int y = num2[j] - '0';
                int result = x * y + add;
                add = result / 10;
                num.push_back('0' + result % 10);
            }
            reverse(num.begin(), num.end());
            if (num != "0")
                ans = addStrings(ans, num + string(multiply, '0'));
            multiply++;
        }
        return ans;
    }
};

2️⃣ 解法二：直接做乘法，长度分别为 m 和 n 的数字相乘，值长度不超过 m + n，vector<int> ansArr(m + n)

/**     	E x a m p l e
 *
 *               9   9   9
 *         ×     6   7   8
 *  ----------------------
 *              72  72  72
 *          63  63  63
 *      54  54  54
 *  ----------------------
 *      54 117 189 135  72
 *  ----------------------
 *      54 117 189 142   2
 *  -----------------------
 *      54 117 203   2   2
 *  -----------------------
 *      54 137   3   2   2
 *  -----------------------
 *      67   7   3   2   2
 *  -----------------------
 *   6   7   7   3   2   2
 */
class Solution {
public:
    string multiply(string num1, string num2) {
        if (num1 == "0" || num2 == "0") {
            return "0";
        }
        int m = num1.length(), n = num2.length();
        vector<int> ansArr(m + n);
        for (int i = m - 1; i >= 0; i--) {
            int x = num1[i] - '0';
            for (int j = n - 1; j >= 0; j--) {
                int y = num2[j] - '0';
                ansArr[i + j + 1] += x * y;
            }
        }
        for (int i = m + n - 1; i > 0; i--) {
            ansArr[i - 1] += ansArr[i] / 10;
            ansArr[i] %= 10;
        }
        int idx = ansArr[0] == 0 ? 1 : 0;
        string ans;
        while (idx < m + n) {
            ans.push_back('0' + ansArr[idx]);
            idx++;
        }
        return ans;
    }
};

239. 滑动窗口最大值

腾讯 WXG 一面

✅ LeetCode: 239. 滑动窗口最大值

给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

返回 滑动窗口中的最大值 。

示例 1：

输入：nums = [1,3,-1,-3,5,3,6,7], k = 3
输出：[3,3,5,5,6,7]
解释：
滑动窗口的位置                最大值
---------------               -----
[1  3  -1] -3  5  3  6  7       3
 1 [3  -1  -3] 5  3  6  7       3
 1  3 [-1  -3  5] 3  6  7       5
 1  3  -1 [-3  5  3] 6  7       5
 1  3  -1  -3 [5  3  6] 7       6
 1  3  -1  -3  5 [3  6  7]      7

1️⃣ 优先队列 priority_queue（记录最大值） + 哈希表（记录删除元素）：self-AC

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        priority_queue<int, vector<int>, less<int>> pq;
        int n = nums.size();
        unordered_map<int, int> cnt;
        for (int i = 0; i < k; i++)
            pq.push(nums[i]);
        vector<int> ans{pq.top()};
        for (int i = k; i < n; i++) {
            cnt[nums[i - k]]++;
            pq.push(nums[i]);
            while (pq.size() > k && cnt[pq.top()] > 0) {
                cnt[pq.top()]--;
                pq.pop();
            }
            ans.push_back(pq.top());
        }
        return ans;
    }
};

2️⃣ 优先队列 priority_queue<pair<int, int>>，通过记录索引值判断 pq.top() 元素是否在定长窗口内

class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        priority_queue<pair<int, int>> pq;
        for (int i = 0; i < k; i++) {
            pq.emplace(nums[i], i);
        }
        vector<int> ans{pq.top().first};
        for (int i = k; i < nums.size(); i++) {
            pq.emplace(nums[i], i);
            while (pq.top().second < i - k + 1) {
                pq.pop();
            }
            ans.push_back(pq.top().first);
        }
        return ans;
    }
};

206. 反转链表

腾讯 WXG 一面

✅ LeetCode: 206. 反转链表

相关例题 —— 92. 反转链表 II：反转部分区间，找到区间 leftNode 与 rightNode，以及 leftNode 左节点 pre 与 rightNode 右节点 nxt，独立区间（断开连接）后反转再接回。

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

示例 1：

1 2	输入：head = [1,2,3,4,5] 输出：[5,4,3,2,1]

1️⃣ 解法一：递归

// 手写链表（LeetCode 已经定义，题目若需要则自己定义）
struct ListNode {
    int val;
    ListNode* next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode* next) : val(x), next(next) {};
};

class Solution {
public:
    // 递归
    ListNode* reverseList(ListNode* head) {
        if (!head || !head->next) {
            return head;
        }
        ListNode* new_head = reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return new_head;
    }
};

2️⃣ 解法二：三指针迭代（pre = nullptr, cur = head, nxt = cur->next）

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }
};

146. LRU 缓存

腾讯 WXG 一面｜腾讯 CSIG 一面｜腾讯 PCG 一面

据说是所有面试中出现概率的 No.1

✅ LeetCode: 146. LRU 缓存、面试题 16.25. LRU 缓存

请你设计并实现一个满足 LRU (最近最少使用) 缓存约束的数据结构。

实现 LRUCache 类：

LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中，则返回关键字的值，否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在，则变更其数据值 value ；如果不存在，则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ，则应该逐出最久未使用的关键字。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1);    // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废，缓存是 {1=1, 3=3}
lRUCache.get(2);    // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废，缓存是 {4=4, 3=3}
lRUCache.get(1);    // 返回 -1 (未找到)
lRUCache.get(3);    // 返回 3
lRUCache.get(4);    // 返回 4

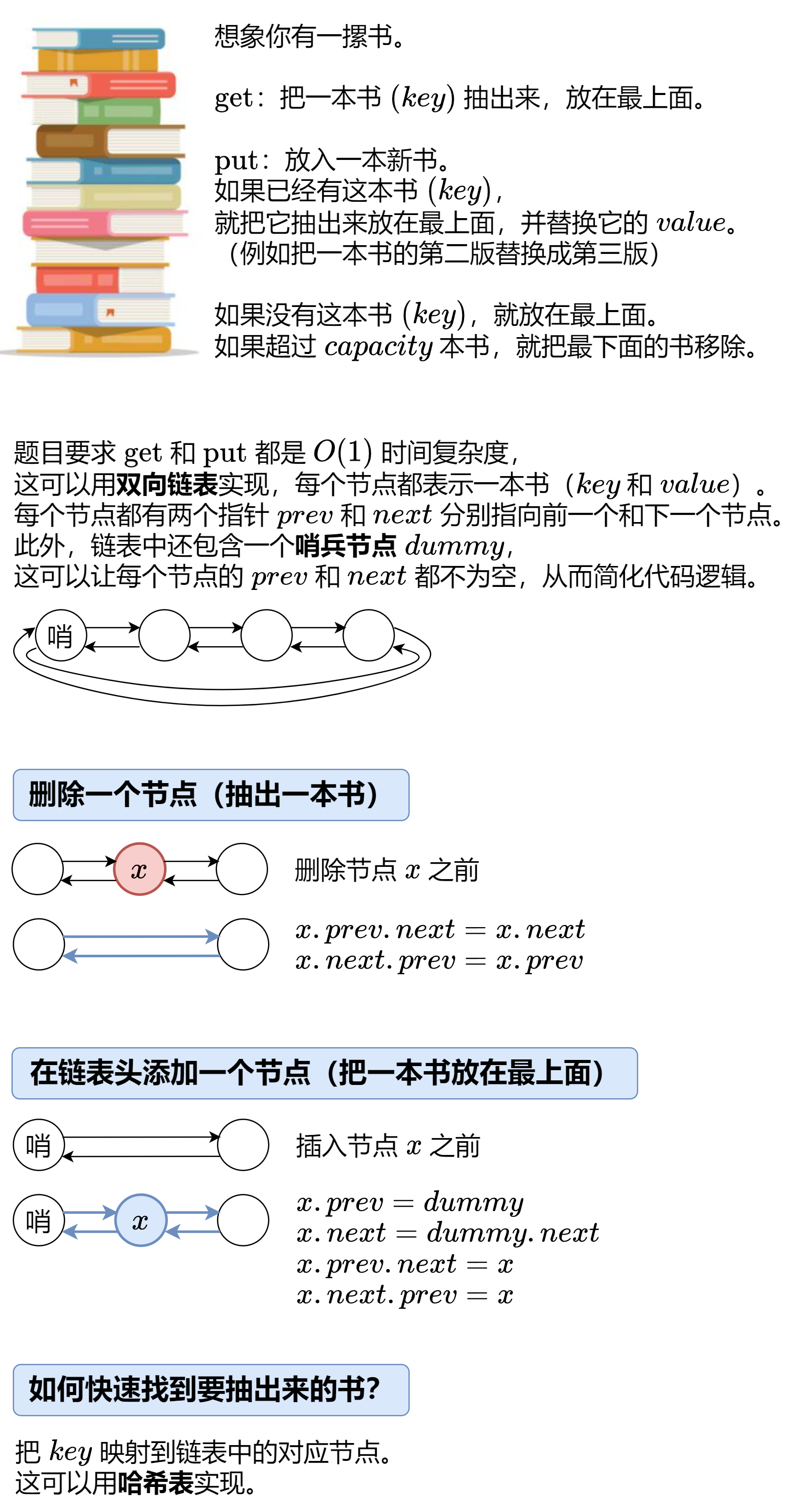
LRUCache：循环双向链表 + 哈希表

循环：方便获取末尾节点进行 LRU 逐出/删除
双向链表
哈希表：快速找到 key 对应的节点

// LRUCache = 循环双向链表 + 哈希表
class Node {
public:
    int key;
    int value;
    Node* prev;
    Node* next;
    Node(int k = 0, int v = 0) : key(k), value(v) {}
};

class LRUCache {
private:
    int capacity;
    Node* dummy;
    unordered_map<int, Node*> key_to_node;

    // 删除一个节点
    void remove(Node* x) {
        x->prev->next = x->next;
        x->next->prev = x->prev;
    }

    // 在链表头添加一个节点
    void push_front(Node* x) {
        x->prev = dummy;
        x->next = dummy->next;
        x->prev->next = x;
        x->next->prev = x;
    }

    // 获取 key 对应的节点, 同时把该节点移到链表头部
    Node* get_node(int key) {
        auto it = key_to_node.find(key);
        if (it == key_to_node.end()) {
            return nullptr;
        }
        Node* node = it->second;
        remove(node);
        push_front(node);
        return node;
    }

public:
    LRUCache(int capacity) : capacity(capacity), dummy(new Node()) {
        // 循环双向链表: 方便取末尾值进行删除
        dummy->prev = dummy;
        dummy->next = dummy;
    }

    int get(int key) {
        Node* node = get_node(key);
        return node ? node->value : -1;
    }

    void put(int key, int value) {
        Node* node = get_node(key);
        if (node) {
            node->value = value;
            return;
        }
        node = new Node(key, value);
        key_to_node[key] = node;
        push_front(node);
        if (key_to_node.size() > capacity) {
            Node* back_node = dummy->prev;
            key_to_node.erase(back_node->key);
            remove(back_node);
            delete back_node;
        }
    }
};

/**
 * Your LRUCache object will be instantiated and called as such:
 * LRUCache* obj = new LRUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

460. LFU 缓存

华为机考

✅ LeetCode: 460. LFU 缓存

相关例题：146. LRU 缓存

请你为最不经常使用（LFU）缓存算法设计并实现数据结构。

实现 LFUCache 类：

LFUCache(int capacity) - 用数据结构的容量 capacity 初始化对象
int get(int key) - 如果键 key 存在于缓存中，则获取键的值，否则返回 -1 。
void put(int key, int value) - 如果键 key 已存在，则变更其值；如果键不存在，请插入键值对。当缓存达到其容量 capacity 时，则应该在插入新项之前，移除最不经常使用的项。在此问题中，当存在平局（即两个或更多个键具有相同使用频率）时，应该去除 最久未使用 的键。

为了确定最不常使用的键，可以为缓存中的每个键维护一个 使用计数器 。使用计数最小的键是最久未使用的键。

当一个键首次插入到缓存中时，它的使用计数器被设置为 1 (由于 put 操作)。对缓存中的键执行 get 或 put 操作，使用计数器的值将会递增。

函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。

示例：

输入：
["LFUCache", "put", "put", "get", "put", "get", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [3], [4, 4], [1], [3], [4]]
输出：
[null, null, null, 1, null, -1, 3, null, -1, 3, 4]

解释：
// cnt(x) = 键 x 的使用计数
// cache=[] 将显示最后一次使用的顺序（最左边的元素是最近的）
LFUCache lfu = new LFUCache(2);
lfu.put(1, 1);   // cache=[1,_], cnt(1)=1
lfu.put(2, 2);   // cache=[2,1], cnt(2)=1, cnt(1)=1
lfu.get(1);      // 返回 1
                 // cache=[1,2], cnt(2)=1, cnt(1)=2
lfu.put(3, 3);   // 去除键 2 ，因为 cnt(2)=1 ，使用计数最小
                 // cache=[3,1], cnt(3)=1, cnt(1)=2
lfu.get(2);      // 返回 -1（未找到）
lfu.get(3);      // 返回 3
                 // cache=[3,1], cnt(3)=2, cnt(1)=2
lfu.put(4, 4);   // 去除键 1 ，1 和 3 的 cnt 相同，但 1 最久未使用
                 // cache=[4,3], cnt(4)=1, cnt(3)=2
lfu.get(1);      // 返回 -1（未找到）
lfu.get(3);      // 返回 3
                 // cache=[3,4], cnt(4)=1, cnt(3)=3
lfu.get(4);      // 返回 4
                 // cache=[3,4], cnt(4)=2, cnt(3)=3

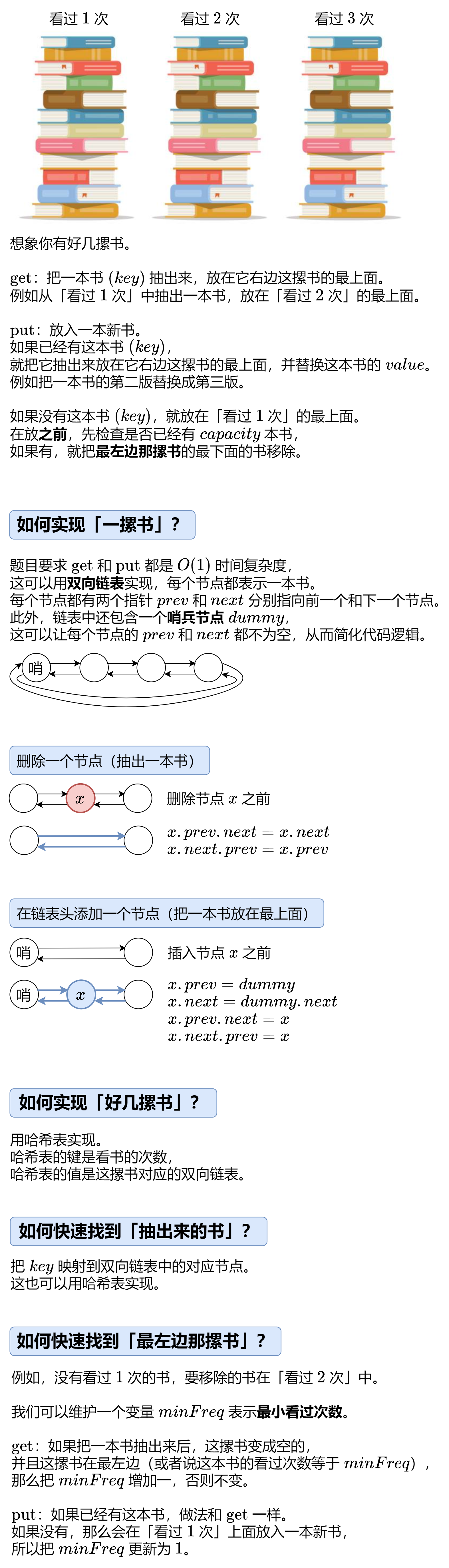
LFU 缓存 = 循环双向链表 + key_to_node 哈希表 + freq_to_dummy 哈希表

class Node {
public:
    int key;
    int value;
    int freq = 1; // default
    Node* prev;
    Node* next;

    Node(int k = 0, int v = 0) : key(k), value(v) {}
};

class LFUCache {
private:
    int min_freq;
    int capacity;
    unordered_map<int, Node*> key_to_node;
    unordered_map<int, Node*> freq_to_dummy; // 每个 freq 代表一个链表的头节点

    // 创新一个新的双向链表
    Node* new_list() {
        Node* dummy = new Node(); // 哨兵节点
        dummy->prev = dummy;
        dummy->next = dummy;
        return dummy;
    }

    void remove(Node* node) {
        node->prev->next = node->next;
        node->next->prev = node->prev;
    }

    void push_front(int freq, Node* node) {
        auto it = freq_to_dummy.find(freq);
        if (it == freq_to_dummy.end()) {
            // pair<iterator, bool> emplace()
            it = freq_to_dummy.emplace(freq, new_list()).first;
        }
        Node* dummy = it->second;
        node->prev = dummy;
        node->next = dummy->next;
        node->prev->next = node;
        node->next->prev = node;
    }

    Node* get_node(int key) {
        auto it = key_to_node.find(key);
        if (it == key_to_node.end()) {
            return nullptr;
        }
        Node* node = it->second;
        remove(node);
        Node* dummy = freq_to_dummy[node->freq];
        if (dummy->prev == dummy) { // 如果该 freq 对应的链表移除 node 后为空时
            freq_to_dummy.erase(node->freq);
            delete dummy;
            if (min_freq == node->freq) { // node->freq 为最小记数
                min_freq++;
            }
        }
        push_front(++node->freq, node);
        return node;
    }

public:
    LFUCache(int capacity) : capacity(capacity) {}

    int get(int key) {
        Node* node = get_node(key);
        return node ? node->value : -1;
    }

    void put(int key, int value) {
        Node* node = get_node(key);
        if (node) {
            node->value = value;
            return;
        }
        if (key_to_node.size() == capacity) {
            Node* dummy = freq_to_dummy[min_freq];
            Node* last_node = dummy->prev;
            key_to_node.erase(last_node->key);
            remove(last_node);
            delete last_node;
            if (dummy->prev == dummy) {
                freq_to_dummy.erase(min_freq);
                delete dummy;
            }
        }
        node = new Node(key, value);
        key_to_node[key] = node;
        push_front(1, node);
        min_freq = 1;
    }
};

/**
 * Your LFUCache object will be instantiated and called as such:
 * LFUCache* obj = new LFUCache(capacity);
 * int param_1 = obj->get(key);
 * obj->put(key,value);
 */

560. 和为 k 的子数组

Momenta 一面

✅ LeetCode: 560. 和为 K 的子数组

给你一个整数数组 nums 和一个整数 k ，请你统计并返回该数组中和为 k 的子数组的个数。

子数组是数组中元素的连续非空序列。

示例 1：

1 2	输入：nums = [1,1,1], k = 2 输出：2

示例 2：

1 2	输入：nums = [1,2,3], k = 3 输出：2

1️⃣ 前缀和 + 哈希表

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int n = nums.size();
        vector<int> preSum(n + 1);
        for(int i = 1; i <= n; i++)
            preSum[i] = nums[i - 1] + preSum[i - 1];
        int ans = 0;
        unordered_map<int, int> cnt;
        for(int num : preSum) {
            ans += cnt.contains(num - k) ? cnt[num - k] : 0;
            cnt[num]++;
        }
        return ans;
    }
};

93. 复原 IP 地址

腾讯 PCG 一面

✅ LeetCode: 93. 复原 IP 地址

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

例如："0.1.2.201" 和 "192.168.1.1" 是有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是无效 IP 地址。

给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你不能重新排序或删除 s 中的任何数字。你可以按任何顺序返回答案。

示例 1：

1 2	输入：s = "25525511135" 输出：["255.255.11.135","255.255.111.35"]

示例 2：

1 2	输入：s = "0000" 输出：["0.0.0.0"]

1️⃣ 解法一：四层循环迭代，简单易懂暴力

class Solution {
public:
    vector<string> restoreIpAddresses(string s) {
        int n = s.length();
        vector<string> ans;
        for (int a = 1; a <= 3; a++) {
            for (int b = 1; b <= 3; b++) {
                for (int c = 1; c <= 3; c++) {
                    for (int d = 1; d <= 3; d++) {
                        if (a + b + c + d == n) {
                            int numA = stoi(s.substr(0, a));
                            int numB = stoi(s.substr(a, b));
                            int numC = stoi(s.substr(a + b, c));
                            int numD = stoi(s.substr(a + b + c, d));
                            if (numA <= 255 && numB <= 255 && numC <= 255 && numD <= 255) {
                                string ip = to_string(numA) + "." +
                                            to_string(numB) + "." +
                                            to_string(numC) + "." +
                                            to_string(numD);
                                if (ip.length() == n + 3) {
                                    ans.push_back(ip);
                                }
                            }
                        }
                    }
                }
            }
        }
        return ans;
    }
};

2️⃣ 回溯法｜递归

// 代码1
class Solution {
public:
    vector<string> ans;
    string ip;

    void backtracking(string s, int i, int segment) {
        if (i == s.length() && segment == 4) {
            ip = ip.substr(0, ip.length() - 1);
            ans.push_back(ip);
            return;
        }
        if (segment > 4) {
            return;
        }
        for (int j = 1; j <= 3 && i + j - 1 < s.length(); j++) {
            if (j > 1 && s[i] == '0') {
                return;
            }
            string subIP = s.substr(i, j);
            int numIP = stoi(subIP);
            if (numIP > 255)
                break;
            int len = ip.length();
            ip = ip + subIP + '.';
            backtracking(s, i + j, segment + 1);
            ip = ip.substr(0, len);
        }
    }

    vector<string> restoreIpAddresses(string s) {
        int n = s.length();
        if (n < 4) {
            return {};
        }
        backtracking(s, 0, 0);
        return ans;
    }
};

// 代码2
class Solution {
public:
    vector<string> ans;
    vector<string> path;

    vector<string> restoreIpAddresses(string s) {
        int n = s.length();
        if (n < 4 || n > 12) {
            return {};
        }

        function<void(int)> dfs = [&](int i) {
            if (i == n && path.size() == 4) {
                string ip = path[0] + "." + path[1] + "." + path[2] + "." + path[3];
                ans.push_back(ip);
                return;
            }
            for (int j = 1; j <= 3 && i + j - 1 < n; j++) {
                string sub = s.substr(i, j);
                if ((j > 1 && s[i] == '0') || stoi(sub) > 255)
                    break;
                path.push_back(sub);
                dfs(i + j);
                path.pop_back();
            }
        };

        dfs(0);

        return ans;
    }
};

25. K 个一组反转链表

腾讯 WXG 一面

✅ LeetCode: 25. K 个一组翻转链表

相关例题 1：24. 两两交换链表中的节点

迭代｜四指针

递归｜三指针

相关例题 2：206. 反转链表

相关例题 3：92. 反转链表 II

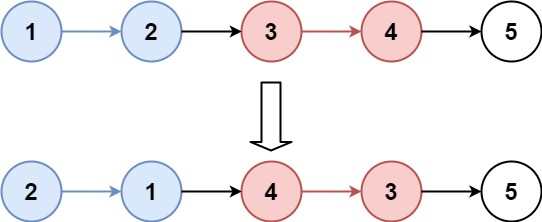
给你链表的头节点 head ，每 k 个节点一组进行翻转，请你返回修改后的链表。

k 是一个正整数，它的值小于或等于链表的长度。如果节点总数不是 k 的整数倍，那么请将最后剩余的节点保持原有顺序。

你不能只是单纯的改变节点内部的值，而是需要实际进行节点交换。

示例 1：

1 2	输入：head = [1,2,3,4,5], k = 2 输出：[2,1,4,3,5]

1️⃣ 解法一：利用「206. 反转链表」+「92. 反转链表 II」完成

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    // 206. 反转链表
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

    // 92. 反转链表 II
    ListNode* reverseBetween(ListNode* head, int left, int right) {
        ListNode dummy(0, head);
        ListNode* pre = &dummy;
        for (int i = 0; i < left - 1; i++) {
            pre = pre->next;
        }
        ListNode* leftNode = pre->next;
        ListNode* rightNode = leftNode;
        for (int i = left; i < right; i++) {
            rightNode = rightNode->next;
        }
        ListNode* nxt = rightNode->next;
        rightNode->next = nullptr;
        reverseList(leftNode);
        pre->next = rightNode;
        leftNode->next = nxt;
        return dummy.next;
    }

    ListNode* reverseKGroup(ListNode* head, int k) {
        int n = 0;
        ListNode* cur = head;
        while (cur) {
            n++;
            cur = cur->next;
        }
        if (n < k) {
            return head;
        }
        ListNode* new_head = head;
        int times = n / k;
        for (int i = 0; times--; i += k) {
            ListNode* node = reverseBetween(new_head, i + 1, i + k);
            if (i == 0) {
                new_head = node;
            }
        }
        return new_head;
    }
};

2️⃣ 解法二｜0x3f：从反转链表直接到「K 个一组翻转链表」

反转过程同「反转链表」代码，从 while (cur) 变成 for (int i = 0; i < k; i++)；其次每处理 k 个一组后，节点之间需要切换（🌟）。

class Solution {
public:
    ListNode* reverseKGroup(ListNode* head, int k) {
        // 统计节点个数
        int n = 0;
        for (ListNode* cur = head; cur; cur = cur->next) {
            n++;
        }
        ListNode dummy(0, head);
        ListNode* p0 = &dummy;
        ListNode* pre = nullptr;
        ListNode* cur = head;
        // k 个一组处理
        for (; n >= k; n -= k) {
            // 同 [206. 反转链表]
            for (int i = 0; i < k; i++) {
                ListNode* nxt = cur->next;
                cur->next = pre;
                pre = cur;
                cur = nxt;
            }
            ListNode* nxt = p0->next;
            p0->next->next = cur;
            p0->next = pre;
            p0 = nxt;
        }
        return dummy.next;
    }
};

234. 回文链表

✅ LeetCode: 234. 回文链表

相关例题：

876. 链表的中间结点

206. 反转链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

示例 1：

1 2	输入：head = [1,2,2,1] 输出：true

先找到中间节点（类 876 题使用快慢指针），然后反转后半段的链表（206 题反转链表），之后逐个比较即可。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    // 876. 链表的中间结点
    ListNode* middleNode(ListNode* head) {
        ListNode *slow = head, *fast = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }
        return slow;
    }

    // 206. 反转链表｜迭代
    ListNode* reverseList(ListNode* head) {
        ListNode* pre = nullptr;
        ListNode* cur = head;
        while (cur) {
            ListNode* nxt = cur->next;
            cur->next = pre;
            pre = cur;
            cur = nxt;
        }
        return pre;
    }

    // 206. 反转链表｜递归
    ListNode* recursion_reverseList(ListNode* head) {
        if (!head || !head->next) {
            return head;
        }
        ListNode* new_head = recursion_reverseList(head->next);
        head->next->next = head;
        head->next = nullptr;
        return new_head;
    }

    bool isPalindrome(ListNode* head) {
        // 中间节点 (偶数则为后一个节点)
        ListNode* middle = middleNode(head);
        ListNode* node = reverseList(middle);
        while (node) {
            if (head->val != node->val) {
                return false;
            }
            head = head->next;
            node = node->next;
        }
        return true;
    }
};

23. 合并 K 个升序链表

快手搜广推一面

✅ LeetCode: 23. 合并 K 个升序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

1️⃣ 最小堆

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeKLists(vector<ListNode*>& lists) {
        auto cmp = [](const ListNode* a, const ListNode* b) {
            return a->val > b->val;
        };
        // decltype 推断表达式类型
        priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq;
        for (auto head : lists) {
            if (head) {
                pq.push(head);
            }
        }
        ListNode dummy{};
        auto cur = &dummy;
        while (!pq.empty()) {
            ListNode* nxt = pq.top();
            pq.pop();
            cur->next = nxt;
            cur = cur->next;
            if (nxt->next) {
                pq.push(nxt->next);
            }
        }
        return dummy.next;
    }
};

2️⃣ 分治法

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
        ListNode dummy{};
        ListNode* cur = &dummy;
        while (list1 && list2) {
            if (list1->val < list2->val) {
                cur->next = list1;
                list1 = list1->next;
            } else {
                cur->next = list2;
                list2 = list2->next;
            }
            cur = cur->next;
        }
        cur->next = list1 ? list1 : list2;
        return dummy.next;
    }

    ListNode* mergeKLists(vector<ListNode*>& lists, int l, int r) {
        if (l == r)
            return lists[l];
        if (l > r)
            return nullptr;
        int m = (l + r) >> 1;
        auto left = mergeKLists(lists, l, m);
        auto right = mergeKLists(lists, m + 1, r);
        return mergeTwoLists(left, right);
    }

    ListNode* mergeKLists(vector<ListNode*>& lists) {
        return mergeKLists(lists, 0, lists.size() - 1);
    }
};

445. 两数相加 II

腾讯 CDG 一面

✅ LeetCode: 445. 两数相加 II

前置题目：

2. 两数相加

206. 反转链表

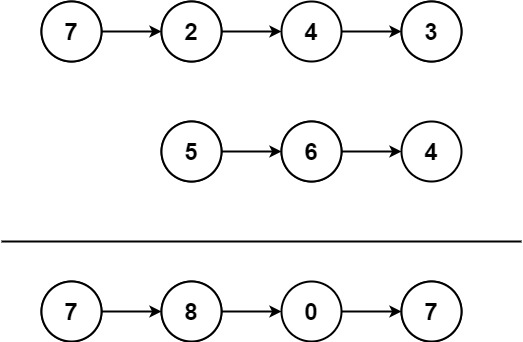
给你两个非空链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。

你可以假设除了数字 0 之外，这两个数字都不会以零开头。

示例1：

1 2	输入：l1 = [7,2,4,3], l2 = [5,6,4] 输出：[7,8,0,7]

反转链表 + 两数相加 = 秒杀

class Solution {
    ListNode* reverseList(ListNode* head) {
        if (head == nullptr || head->next == nullptr) {
            return head;
        }
        auto new_head = reverseList(head->next);
        head->next->next = head; // 把下一个节点指向自己
        head->next = nullptr; // 断开指向下一个节点的连接，保证最终链表的末尾节点的 next 是空节点
        return new_head;
    }

    // l1 和 l2 为当前遍历的节点，carry 为进位
    ListNode* addTwo(ListNode* l1, ListNode* l2, int carry = 0) {
        if (l1 == nullptr && l2 == nullptr) { // 递归边界：l1 和 l2 都是空节点
            return carry ? new ListNode(carry) : nullptr; // 如果进位了，就额外创建一个节点
        }
        if (l1 == nullptr) { // 如果 l1 是空的，那么此时 l2 一定不是空节点
            swap(l1, l2); // 交换 l1 与 l2，保证 l1 非空，从而简化代码
        }
        carry += l1->val + (l2 ? l2->val : 0); // 节点值和进位加在一起
        l1->val = carry % 10; // 每个节点保存一个数位
        l1->next = addTwo(l1->next, (l2 ? l2->next : nullptr), carry / 10); // 进位
        return l1;
    }

public:
    ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
        l1 = reverseList(l1);
        l2 = reverseList(l2); // l1 和 l2 反转后，就变成【2. 两数相加】了
        auto l3 = addTwo(l1, l2);
        return reverseList(l3);
    }
};

24. 两两交换链表中的节点

腾讯 CSIG 一面

✅ LeetCode: 24. 两两交换链表中的节点

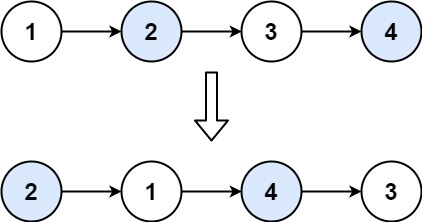
给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

示例 1：

1 2	输入：head = [1,2,3,4] 输出：[2,1,4,3]

四个指针秒了

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
class Solution {
public:
    ListNode* swapPairs(ListNode* head) {
        if (!head)
            return head;
        ListNode dummy(0, head);
        ListNode* node0 = &dummy;
        ListNode* node1 = head;
        while (node1 && node1->next) {
            ListNode* node2 = node1->next;
            ListNode* node3 = node2->next;
            node2->next = node1;
            node1->next = node3;
            node0->next = node2;
            node0 = node1;
            node1 = node3;
        }
        return dummy.next;
    }
};

72. 编辑距离

腾讯 CDG 一面

✅ LeetCode: 72. 编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符
删除一个字符
替换一个字符

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

递推｜注意边界初始化值

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.length(), n = word2.length();
        vector<vector<int>> f(m + 1, vector<int>(n + 1));
        for (int i = 0; i <= m; i++)
            f[i][0] = i;
        for (int j = 0; j <= n; j++)
            f[0][j] = j;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                f[i + 1][j + 1] = word1[i] == word2[j] ? f[i][j] : min({f[i][j], f[i + 1][j], f[i][j + 1]}) + 1;
            }
        }
        return f[m][n];
    }
};

4. 寻找两个正序数组的中位数

字节 AML 一面

✅ LeetCode: 4. 寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

1
2
3

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

1
2
3

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

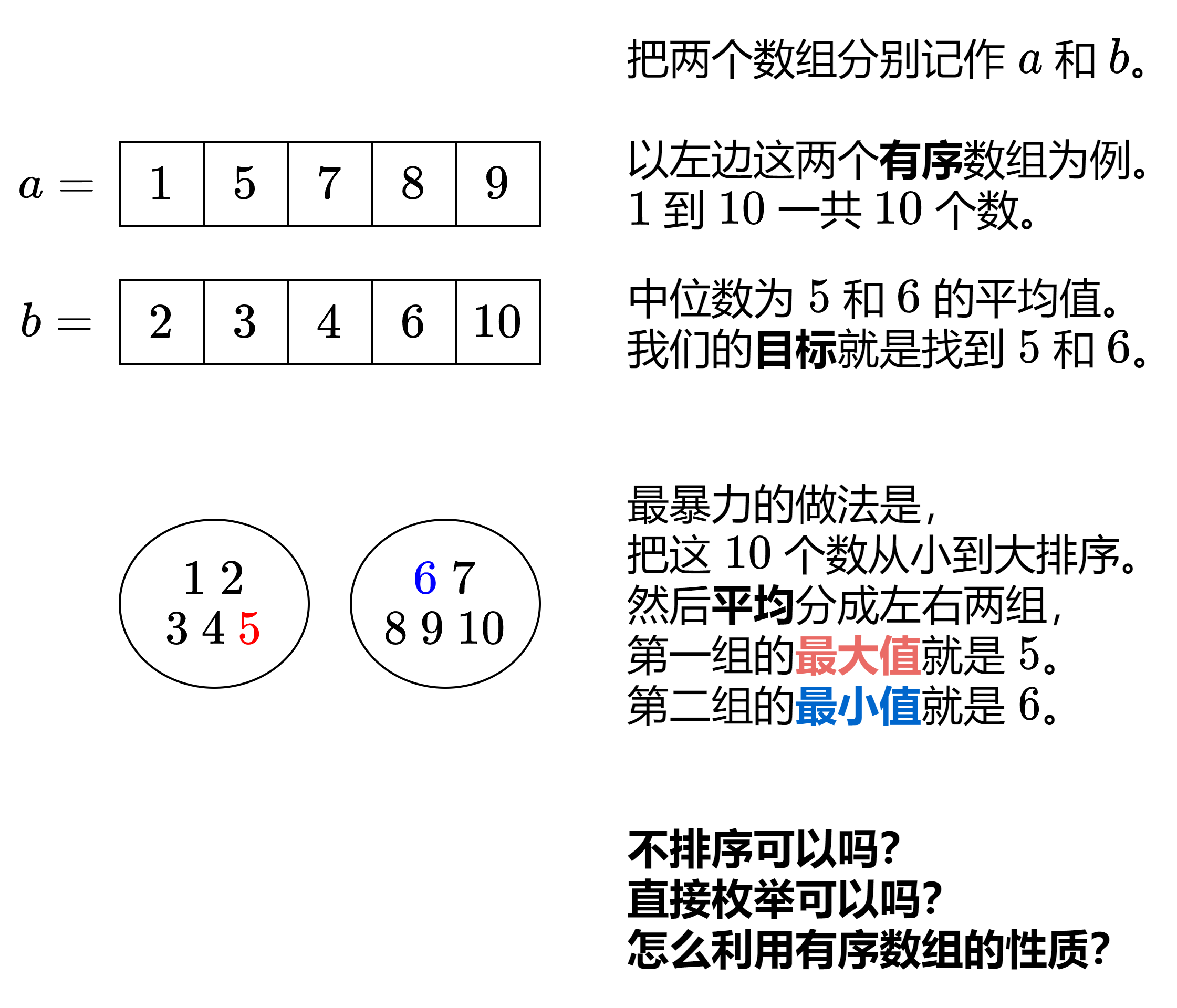
🧐 分析

本质上，我们需要在两个有序数组中，查找第 k 小的数，其中 k = (m + n) / 2 取上整。

如果 m+n 是奇数，返回第 k 小的数。
如果 m+n 是偶数，返回第 k 小的数和第 k+1 小的数的平均值。

先从最暴力的「排序」做法开始，然后讲解「双指针」做法，最后过渡到「二分查找」做法。

🙋 答疑

1️⃣ 相向双指针｜均匀分组｜当条件「第一组最大值 <= 第二组最小值」满足

class Solution {
public:
    // 相向双指针｜均匀分组｜当条件「第一组最大值 <= 第二组最小值」满足
    // Hot 100 中最难的一题
    double findMedianSortedArrays(vector<int>& a, vector<int>& b) {
        if (a.size() > b.size())
            swap(a, b);
        int m = a.size(), n = b.size();
        a.insert(a.begin(), INT_MIN);
        b.insert(b.begin(), INT_MIN);
        a.push_back(INT_MAX);
        b.push_back(INT_MAX);

        int i = 0, j = (m + n + 1) / 2;
        while (true) {
            if (a[i] <= b[j + 1] && b[j] <= a[i + 1]) {
                int max1 = max(a[i], b[j]);         // 第一组最大值
                int min2 = min(a[i + 1], b[j + 1]); // 第二组最小值
                return (m + n) % 2 ? max1 : (max1 + min2) / 2.0;
            }
            i++;
            j--;
        }
    }
};

2️⃣ 用二分查找优化：由于满足点只有一个, 所以判断条件为 $a[i] <= b[j + 1]$

class Solution {
public:
    // 二分优化, 由于满足点只有一个, 所以判断条件为 a[i] <= b[j + 1]
    double findMedianSortedArrays(vector<int>& a, vector<int>& b) {
        if (a.size() > b.size())
            swap(a, b);
        int m = a.size(), n = b.size();
        a.insert(a.begin(), INT_MIN);
        b.insert(b.begin(), INT_MIN);
        a.push_back(INT_MAX);
        b.push_back(INT_MAX);

        int left = 0, right = m + 1;
        while (left + 1 < right) {
            int i = (left + right) / 2;
            int j = (m + n + 1) / 2 - i;
            if (a[i] <= b[j + 1]) {
                left = i;
            } else {
                right = i;
            }
        }

        // left == right - 1
        int i = left;
        int j = (m + n + 1) / 2 - i;
        int max1 = max(a[i], b[j]);
        int min2 = min(a[i + 1], b[j + 1]);
        return (m + n) % 2 ? max1 : (max1 + min2) / 2.0;
    }
};

230. 二叉搜索树中第 K 小的元素

腾讯 WXG 一面

✅ LeetCode：230. 二叉搜索树中第 K 小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 小的元素（从 1 开始计数）。

示例 1：

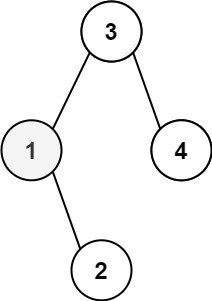
1 2	输入：root = [3,1,4,null,2], k = 1 输出：1

1️⃣ 中序遍历：在中序遍历，即「左-根-右」的过程中，每次递归完左子树，就把 k 减少 1，表示我们按照中序遍历访问到了一个节点。如果减一后 k 变成 0，那么答案就是当前节点的值，用一个外部变量 ans 记录。

class Solution {
public:
    int kthSmallest(TreeNode* root, int k) {
        int ans;
        auto dfs = [&](this auto&& dfs, TreeNode* node) -> void {
            if (node == nullptr) {
                return;
            }
            dfs(node->left); // 左
            if (--k == 0) {
                ans = node->val; // 根
            }
            dfs(node->right); // 右
        };
        dfs(root);
        return ans;
    }
};

2️⃣ 中序遍历：直接将所有答案记录到 vector 数组中，返回对应索引值即可。

class Solution {
public:
    vector<int> ans;

    void preOrder(TreeNode* node) {
        if (node == nullptr)
            return;
        preOrder(node->left);
        ans.push_back(node->val);
        preOrder(node->right);
    }

    int kthSmallest(TreeNode* root, int k) {
        preOrder(root);
        return ans[k - 1];
    }
};

354. 俄罗斯套娃信封问题

腾讯 WXG 一面

✅ LeetCode：354. 俄罗斯套娃信封问题

给你一个二维整数数组 envelopes ，其中 envelopes[i] = [wi, hi] ，表示第 i 个信封的宽度和高度。

当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。

请计算 最多能有多少个 信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

注意：不允许旋转信封。

示例 1：

1
2
3

输入：envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出：3
解释：最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

示例 2：

1 2	输入：envelopes = [[1,1],[1,1],[1,1]] 输出：1

0️⃣ DP 会超时，只能用二分查找。

1️⃣ 贪心 + 二分查找：先排序，再按照 LIS 二分贪心模板求最长递增子序列。因为二者都必须是递增的，所以第二维度需要逆序排序，使得第一维度相同的多个数，最后一个插入的一定是最小值，这样能嵌套的信封最多。

class Solution {
public:
    int maxEnvelopes(vector<vector<int>>& envelopes) {
        sort(envelopes.begin(), envelopes.end(), [](const auto& a, const auto& b) {
            return a[0] < b[0] || (a[0] == b[0] && a[1] > b[1]);
        });
        vector<int> g;
        for (auto& e : envelopes) {
            auto it = lower_bound(g.begin(), g.end(), e[1]);
            if (it == g.end()) {
                g.push_back(e[1]);
            } else {
                *it = e[1];
            }
        }
        return g.size();
    }
};

本文由 Yikun Wu 原创，采用 CC BY-NC-SA 4.0 许可协议，转载请注明出处。

✍️ 八股文 @ 面试手撕

415. 大数相加

43. 大数相乘

239. 滑动窗口最大值

206. 反转链表

146. LRU 缓存

460. LFU 缓存

560. 和为 k 的子数组

93. 复原 IP 地址

25. K 个一组反转链表

234. 回文链表

23. 合并 K 个升序链表

445. 两数相加 II

24. 两两交换链表中的节点

72. 编辑距离

4. 寻找两个正序数组的中位数

🧐 分析

🙋 答疑

1️⃣ 相向双指针｜均匀分组｜当条件「第一组最大值 <= 第二组最小值」满足

2️⃣ 用二分查找优化： 由于满足点只有一个, 所以判断条件为 $a[i] <= b[j + 1]$

230. 二叉搜索树中第 K 小的元素

354. 俄罗斯套娃信封问题

2️⃣ 用二分查找优化：由于满足点只有一个, 所以判断条件为 $a[i] <= b[j + 1]$